Shortest path

Dijkstra’salgorithm

• Dijkstra’s algorithm (pronounced dyke – strah) is a method of finding the shortest path between two points on a graph.

• Each point on the graph is called a node or a vertex (for more information on the features and uses of graphs, see Chapter 19).

• It is the basis of technology such as GPS tracking and, therefore, is an important part of AI.

• This set of instructions briefly describes how it works.

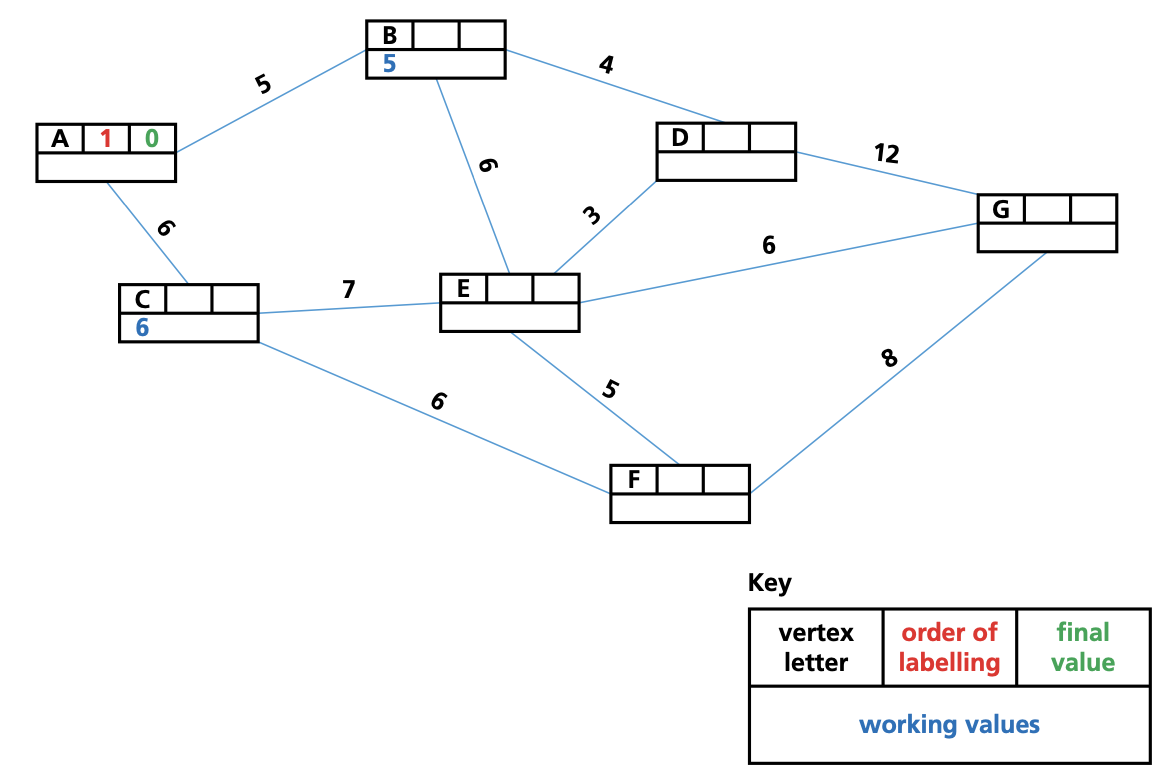
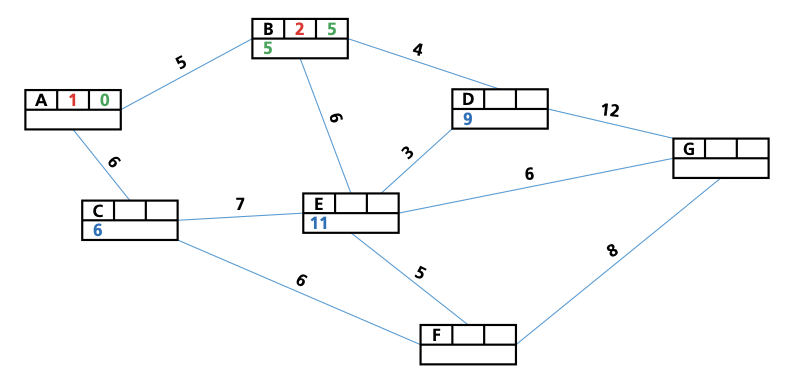
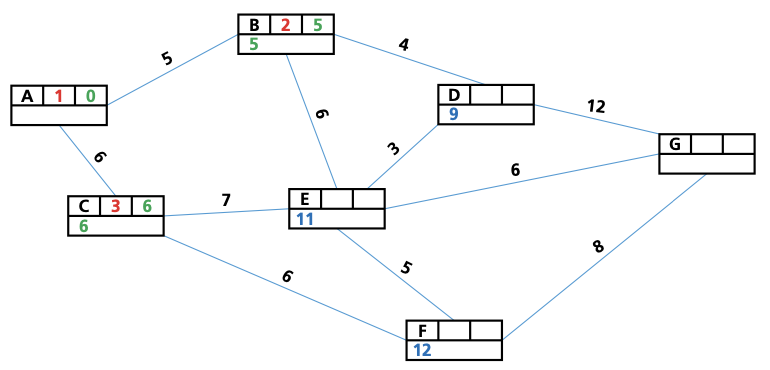
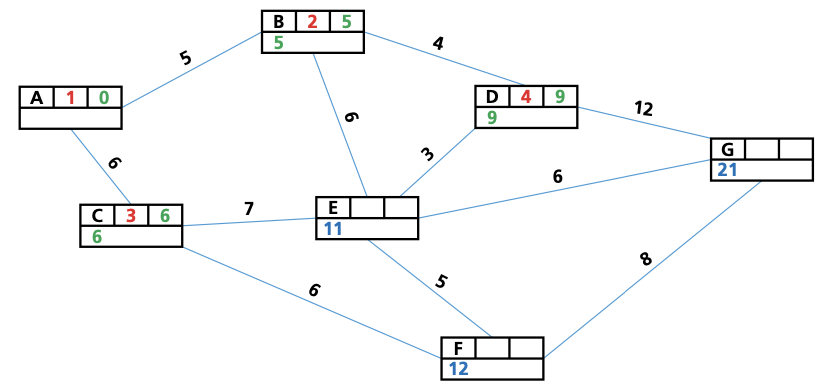
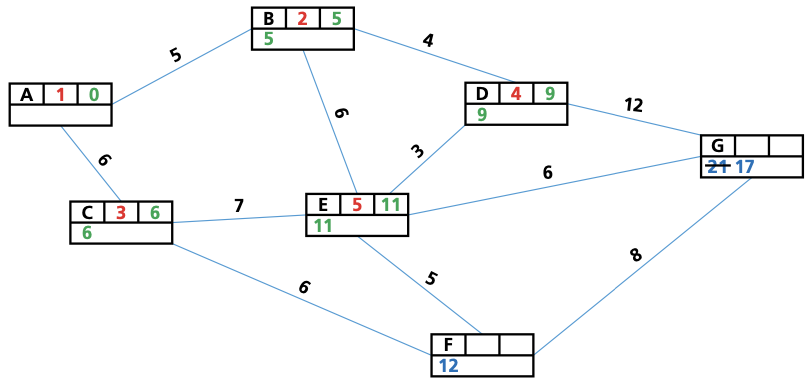
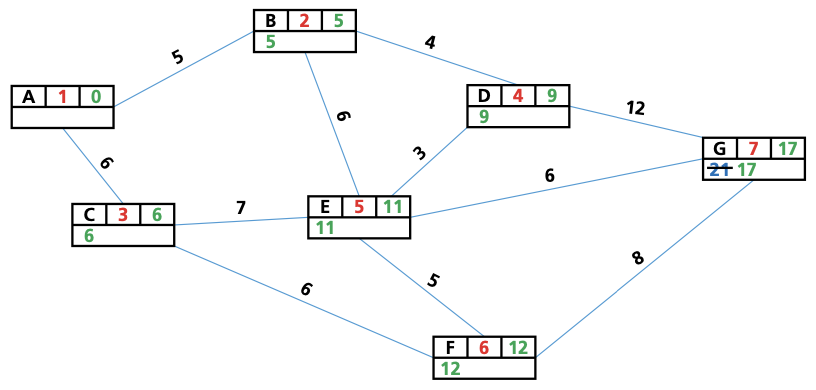
  1. Give the start vertex a final value of 0.
  2. Give each vertex connected to the vertex we have just given a final value to(in the first instance, this is the start vertex) a working (temporary) value.If a vertex already has a working value, only replace it with another working value if it is a lower value.
  3. Check the working value of any vertex that has not yet been assigned a final value. Assign the smallest value to this vertex; this is now its final value.
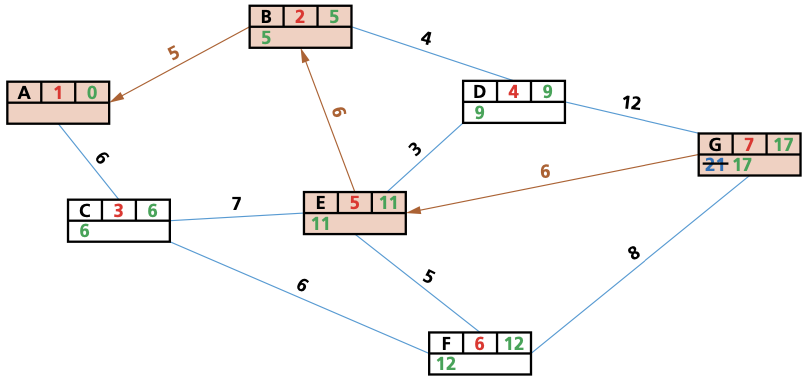
  4. Repeat steps 2 and 3 until the end vertex is reached, and all vertices have been assigned a final value.
  5. Trace the route back from the end vertex to the start vertex to find the shortest path between these two vertices.

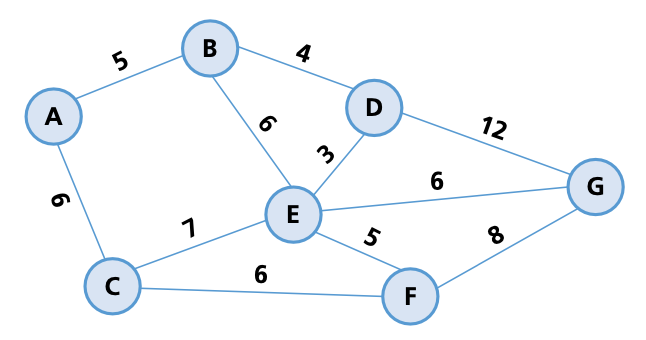
• First, redraw the diagram, replacing the circled letters as per the key:

---

---

---

---

---

---

A* algorithm

• Dijkstra’s algorithm simply checks each vertex looking for the shortest path, even if that takes you away from your destination – it pays no attention to direction.
• With larger, more complex problems, that can be a time-consuming drawback.
• A* algorithm is based on Dijkstra, but adds an extra heuristic (h) value – an ‘intelligent guess’ on how far we have to go to reach the destination most efficiently.

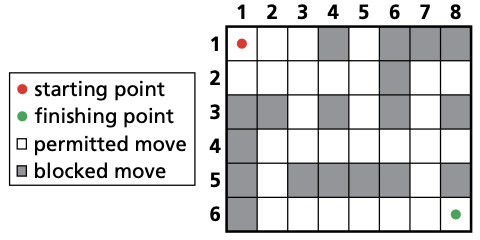
• Each of the parts of the graph are called nodes (or vertices). Each node has four values
  • h (the heuristic value)
  • g (movement cost)
  • f (sum of g and h values)
  • n (previous node in the path)

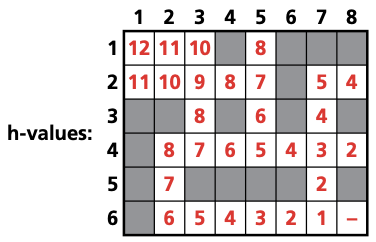
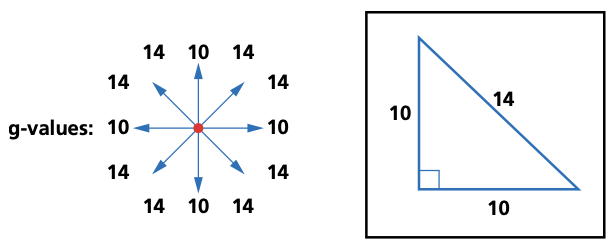
• Find the f values using f(n) = g(n) + h(n).

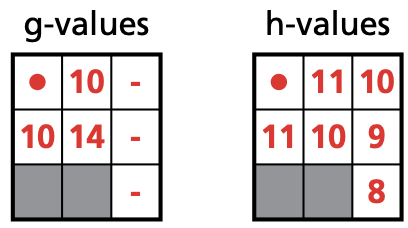
• square (1,2): f = 10 + 11 = 21
• square (2,1): f = 10 + 11 = 21
• square (2,2): f = 14 + 10 = 24

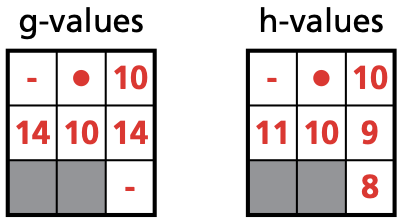
• square (3,1): f = 10 + 10 = 20
• square (3,2): f = 14 + 9 = 23
• square (1,2): f = 14 + 11 = 25
• square (2,2): f = 10 + 10 = 20

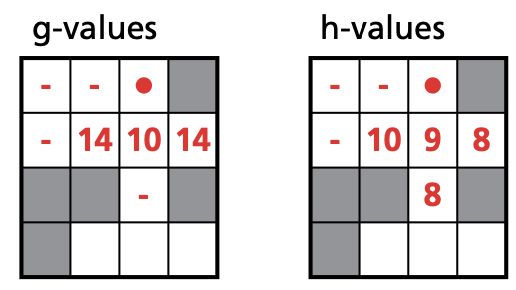
• square (2,2): f = 14 + 10 = 24
• square (3,2): f = 10 + 9 = 19
• square (4,2): f = 14 + 8 = 22

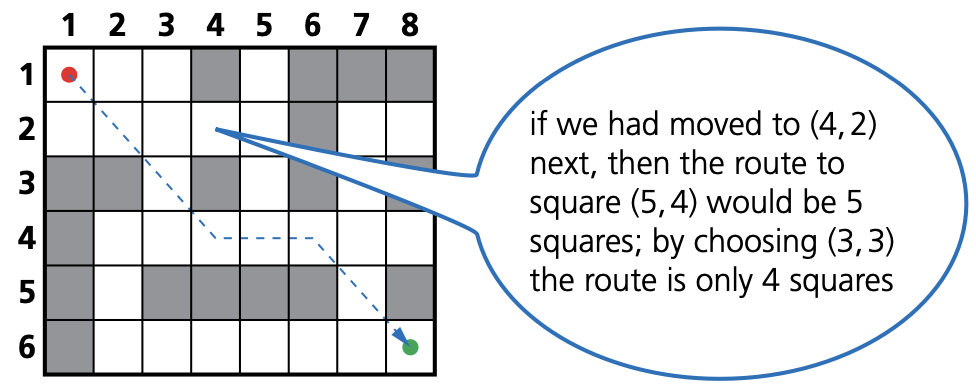
• The shortest path is:
• (1,1) → (2,2) → (3,3) → (4,4) → (5,4) → (6,4) → (7,5) → (8,6)